
Cricket, often considered a game of uncertainties, is not only about bat and ball but also about the unpredictable elements that can influence the course of a match. One such element is the weather, and when rain interrupts play, the Duckworth-Lewis Method (now DLS) steps onto the stage.
Widely used in limited-overs formats, DLS aims to adjust targets in rain-affected matches, ensuring fairness and excitement for players and fans alike.
In this blog, for our math geeks, we’ll dive into the intricacies of the Duckworth-Lewis Method (now DLS) and attempt to demystify its calculations.
Calculations:
The essence of the DLS method is ‘resources’. Each team has two ‘resources’ to score as many runs as possible:
- The number of overs they have left
- The number of wickets they have in hand
At any given time in any innings, a team’s ability to score more runs depends on the combination of these two resources they have left.
The entire calculation of the DLS method is based on the table given below:
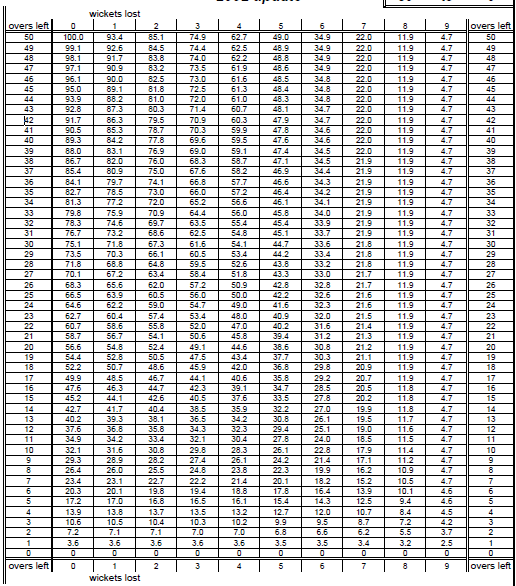
The first and the last column represent the overs left while the first and the last row represent wickets left. The values in between represent the percentage of resources consumed.
Scenarios
The DLS method is used to calculated the “par score” for team 2 in rain interrupted matches. This method comes into play in 2 scenarios:
- Team 1’s innings is cut short due to rain and now both teams will play less than 50 overs.
- Team 1’s innings is completed and Team 2’s innings is cut short due to rain, which means only team 2 will play less than 50 overs.
In scenario 1, team 2 will have an increased target, which means a target more than the score team 1 has made. The rationale behind this is that team 1 did not know that it’s resources were going to get reduced due to rain, while team 2 knows right from the start how many resources it has.
In scenario 2, team 2 will have a reduced target. We will dive deeper into both the scenarios later in this blog.
Steps:
The par score for team 2 can be calculated using the below 2 steps:
Step 1: Calculate Team 1’s resources (R1) and team 2’s resources (R2) with the help of Table 1
Below is the formula for resources available:
Total resources available = 100% − Resources remaining at 1st interruption + Resources remaining at 1st restart − Resources remaining at 2nd interruption + Resources remaining at 2nd restart − Resources remaining at 3rd interruption + Resources remaining at 3rd restart…
Let us take an example of England tour of India 2008, 4th ODI
- Rain stopped play when India had reached 82–1 from 14 overs (i.e. 36 remaining). At the restart both innings were reduced to 44 overs (i.e. 30 remaining for India)
- Rain stopped play again when India had reached 106–1 from 17 overs (i.e. 27 remaining), and at the restart both innings were reduced further to 22 overs (i.e. 5 remaining for India)
- India finished on 166–4 from their 22 overs
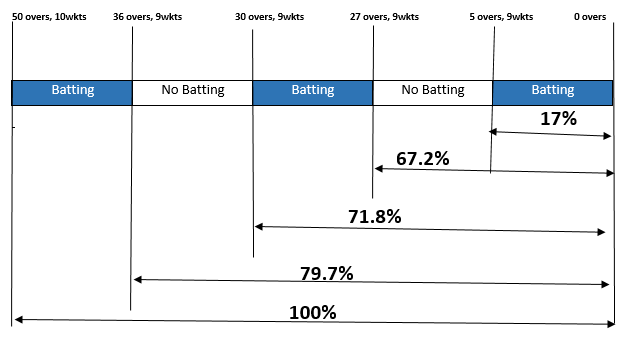
These percentage resources values are taken from Table 1
Thus according to the formula, the resources available with India (R1) = 100%-79.7%+71.8%-67.2%+17%=41.9%
Resources available with England (R2)= 60.7% (22 overs and 10 wickets)
Step 2: Apply the following formula used to calculate team 2’s par score:
Case 1: When R2<R1
Team 2’s par score = Team 1’s score x (Team 2’s resources/Team 1’s resources)
Case 2: When R2>R1
Team 2’s par score = S + G50 x (R2-R1)/100
where G50 is the average score expected from the team batting first in an uninterrupted 50 overs-per-innings match. Below is the G50 table
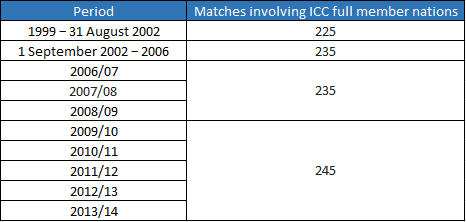
Case 3: When R2 = R1, no adjustment to Team 2’s target score is needed.
We will understand the complete calculation with the help of 2 examples.
Examples:
Increased target: Multiple interruptions in Team 1’s innings; Team 2’s innings completed.
This is scenario 1 mentioned earlier in this blog. Team 2 will have an increased target if team 1’s innings is interrupted either at the start, end or multiple times in the middle.
We will take the most complex example, i.e. when the innings is interrupted multiple times in the middle.
We will continue the example of England tour of India 2008, 4th ODI
- Rain stopped play when India had reached 82–1 from 14 overs (i.e. 36 remaining). At the restart both innings were reduced to 44 overs (i.e. 30 remaining for India)
- Rain stopped play again when India had reached 106–1 from 17 overs (i.e. 27 remaining), and at the restart both innings were reduced further to 22 overs (i.e. 5 remaining for India)
- India finished on 166–4 from their 22 overs

England could manage 178 in their 22 overs, and thus India won the match.
Reduced target: Team 1’s innings completed; Team 2’s innings interrupted:
In 2003, when Sri Lanka played South Africa in the World Cup, Sri Lanka batted first and scored 268–9 from their 50 overs. Chasing a target of 269, South Africa had reached 229–6 from 45 overs when play was abandoned.

Since South Africa’s score matched the DLS par score, the match was declared as tied.
Strategy: Conservative or Aggressive?
So when there are chances of rain, should a team bat conservatively and save wickets, or should the bat aggressively without caring about wickets?
Team 1
Suppose Team 1 has been batting without interruptions, but thinks the innings will be cut short at 35 overs, i.e. with 15 overs left.
Then Team 2 will have 35 overs to bat, so Team 2’s resource will be 82.7% (refer Table 1). Team 1 thinks by batting conservatively it can reach 150–6, or by batting aggressively it can reach 180–8:
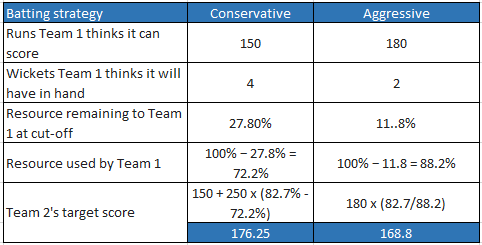
Therefore, in this case, the conservative strategy achieves a higher target for Team 2.
However, suppose instead that the difference between the two strategies is scoring 150–2 or 180–4:
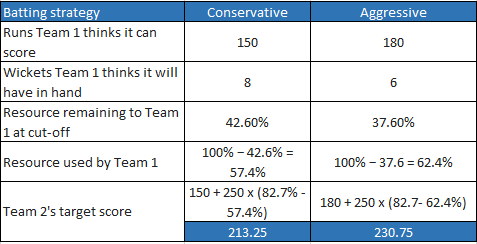
In this case, the aggressive strategy is better.
Team 2:
As an example, in the 2003 Cricket World Cup Final Australia batted first and scored 359 from 50 overs.
As Australia completed their 50 overs, their total resources used R1=100%, so India’s par score throughout their innings was: 359 x R2/100%, where R2 is the amount of resource used to that point.
As shown in the first line of the table below, after 9 overs India were 57-1, and 41 overs and 9 wickets remaining equates to 85.3% of resources, so 100% − 85.3% = 14.7% had been used. India’s par score after 9 overs was therefore 359 x 14.7%/100% = 52.773, which is rounded down to 52.
The par score goes on increasing with every ball bowled and every wicket lost, as the amount of resource used increases.
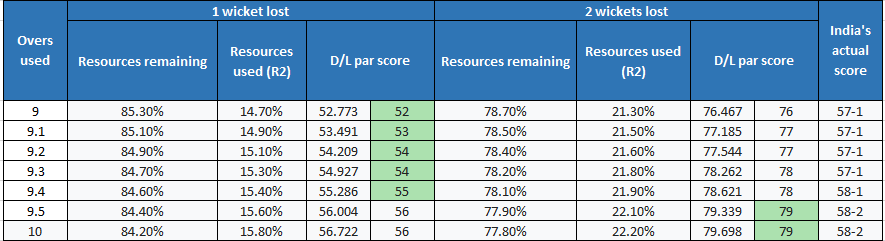
At 9.5 overs, India lost another wicket which is when the par score jumped from 55 to 79. Had rain affected the match at this moment, India would have lost the match in just a matter of 1 ball.
Conclusion:
The Duckworth-Lewis Stern method has become an integral part of limited-overs cricket, providing a fair means of determining revised targets in rain-affected matches.
The objective is simple – to ensure that the impact of weather interruptions is minimized, and matches can still produce decisive outcomes.
See you onto the next one, Sayonara!